Synthetic Data

Defines methods for generating synthetic data with varying levels of realism.

Generating Activity from Light Schedules

This function generates an ‘activity’ schedule from an input LightSchedule.

It essentially corrupts the light pulse train based on three normal distributions. When the light pulse is on, the function draws from a high or low activity distribution based on a parameter representing how active the person is, and when it is off, the function draws from a sleep activity distribution.

There are 7 parameters for the method: * mu_l - mean low activity level * mu_h - mean high activity level * mu_s - mean sleep activity level * sigma_l - std of high activity level * sigma_h - std of high activity level * sigma_s - std of sleep activity - how active the person is in their sleep * active_level - [0, 1] value representing how active the person is. When close to 1, they have a higher probability of being in the high activity distribution at any point in time

Examples

This section uses the Circadian package to generate the 4 light schedules: * Regular * Shift Work * Slam Shift * Social Jetlag

then passes each to the function to generate ‘activity’ schedules from them.

# Activity levels.
mu_l = 5    # Mean of low activity levels.
mu_h = 25   # Mean of high activity levels.
mu_s = 0    # Mean of sleep activity levels.

# Activity uncertainty.
sigma_l = 7.5   # Std of low activity levels.
sigma_h = 30    # Std of high activity levels.
sigma_s = 2     # Std of activity during sleep.
sigma_t = 1.5   # Std of sleep onset/offset timing.

# The person's activity level from 0 to 1.
active_level = 0.5

# Number of days and samples of interest.
num_days = 12
num_samples = 60*24*num_days
# Create the time, light and activity signals.

# Time vector.
time = np.arange(0, 24*num_days, 1/60)

# Light schedules.
regular_light = LightSchedule.Regular()
shift_light = LightSchedule.ShiftWork()
slam_light = LightSchedule.SlamShift()
social_jetlag = LightSchedule.SocialJetlag()

# Create the activity signals.
regular_activity = generate_activity_from_light(
    time, regular_light,
    mu_l, mu_h, mu_s, sigma_l, sigma_h, sigma_s,
    active_level, 
)
shift_activity = generate_activity_from_light(
    time, shift_light,
    mu_l, mu_h, mu_s, sigma_l, sigma_h, sigma_s,
    active_level,
)
slam_activity = generate_activity_from_light(
    time, slam_light,
    mu_l, mu_h, mu_s, sigma_l, sigma_h, sigma_s,
    active_level,
)
social_jetlag_activity = generate_activity_from_light(
    time, social_jetlag,
    mu_l, mu_h, mu_s, sigma_l, sigma_h, sigma_s,
    active_level
)

Visualization

Here, we visualize the ‘activity’ schedules with their corresponding input light schedules.

nrows, ncols = 2, 1
# Regular plots.
fig, ax = plt.subplots(nrows=nrows, ncols=ncols)
regular_light.plot(
    plot_start_time=0.0,
    plot_end_time=24*num_days,
    num_samples=num_samples,
    ax=ax[0]
)
ax[0].set_ylabel("Light (lux)")
ax[0].set_title("Regular Light Schedule")
ax[0].set_xticks(np.arange(min(time), max(time), 24))
ax[0].grid()
ax[1].plot(
    time, regular_activity
)
ax[1].set_ylabel("Activity (steps/min)")
ax[1].set_xlabel("Time (hours)")
ax[1].set_title("Regular Activity Schedule")
ax[1].set_xticks(np.arange(min(time), max(time), 24))
ax[1].grid()

plt.tight_layout()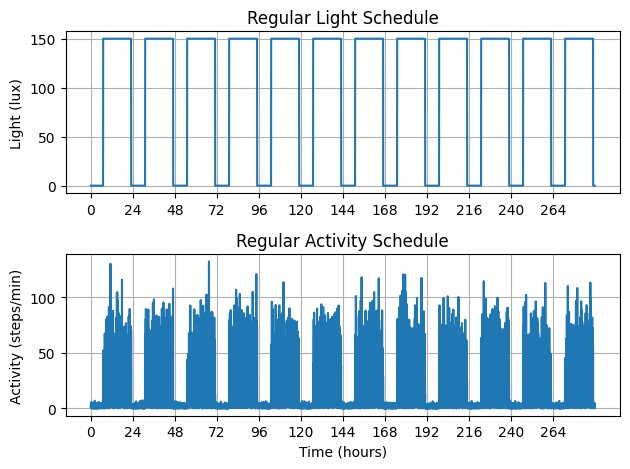

# Shift Work plots.
fig, ax = plt.subplots(nrows=nrows, ncols=ncols)
shift_light.plot(
    plot_start_time=0.0,
    plot_end_time=24*num_days,
    num_samples=num_samples,
    ax=ax[0]
)
ax[0].set_ylabel("Light (lux)")
ax[0].set_title("Shift Work Light Schedule")
ax[0].set_xticks(np.arange(min(time), max(time), 24))
ax[0].grid()
ax[1].plot(
    time, shift_activity
)
ax[1].set_ylabel("Activity (steps/min)")
ax[1].set_xlabel("Time (hours)")
ax[1].set_title("Shift Work Activity Schedule")
ax[1].set_xticks(np.arange(min(time), max(time), 24))
ax[1].grid()

plt.tight_layout()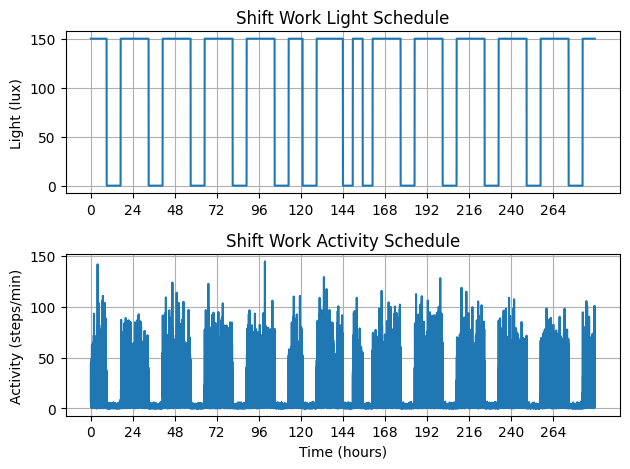

# Slam Shift plots.
fig, ax = plt.subplots(nrows=nrows, ncols=ncols)
slam_light.plot(
    plot_start_time=0.0,
    plot_end_time=24*num_days,
    num_samples=num_samples,
    ax=ax[0]
)
ax[0].set_ylabel("Light (lux)")
ax[0].set_title("Slam Shift Light Schedule")
ax[0].set_xticks(np.arange(min(time), max(time), 24))
ax[0].grid()
ax[1].plot(
    time, slam_activity
)
ax[1].set_ylabel("Activity (steps/min)")
ax[1].set_xlabel("Time (hours)")
ax[1].set_title("Slam Shift Activity Schedule")
ax[1].set_xticks(np.arange(min(time), max(time), 24))
ax[1].grid()

plt.tight_layout()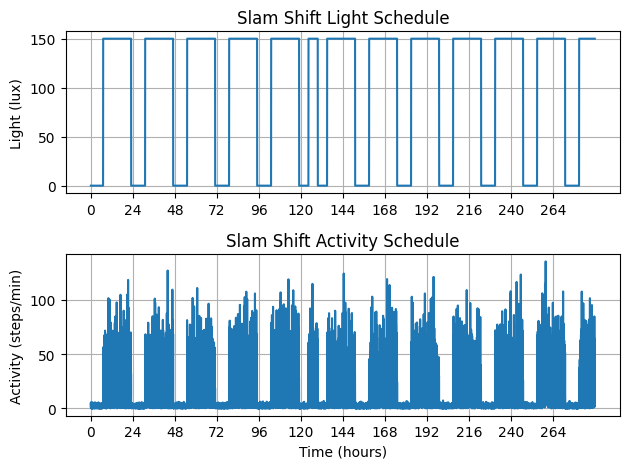

# Social Jetlag plots.
fig, ax = plt.subplots(nrows=nrows, ncols=ncols)
social_jetlag.plot(
    plot_start_time=0.0,
    plot_end_time=24*num_days,
    num_samples=num_samples,
    ax=ax[0]
)
ax[0].set_ylabel("Light (lux)")
ax[0].set_title("Social Jetlag Light Schedule")
ax[0].set_xticks(np.arange(min(time), max(time), 24))
ax[0].grid()
ax[1].plot(
    time, social_jetlag_activity
)
ax[1].set_ylabel("Activity (steps/min)")
ax[1].set_xlabel("Time (hours)")
ax[1].set_title("Social Jetlag Activity Schedule")
ax[1].set_xticks(np.arange(min(time), max(time), 24))
ax[1].grid()

plt.tight_layout()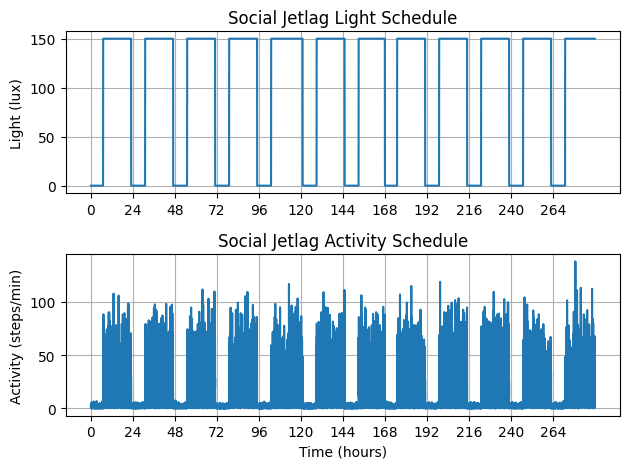

API Documentation

source

generate_activity_from_light

 generate_activity_from_light (time:numpy.ndarray,
                               light:circadian.lights.LightSchedule,
                               mu_l:float=5.0, mu_h:float=25.0,
                               mu_s:float=0.0, sigma_l:float=7.5,
                               sigma_h:float=30.0, sigma_s:float=2.0,
                               active_level:float=0.5)

Generates an ‘activity’ schedule from an input light schedule. The activity schedule produced is a corrupted version of the light schedule.

Type Default Details
time ndarray time points.
light LightSchedule light schedule.
mu_l float 5.0 mean of low activity levels.
mu_h float 25.0 mean of high activity levels.
mu_s float 0.0 mean of sleep activity levels.
sigma_l float 7.5 std of low activity levels.
sigma_h float 30.0 std of high activity levels.
sigma_s float 2.0 std of activity during sleep.
active_level float 0.5 person’s activity level from 0 to 1. Represents the probability of choosing from the high or low activity distributions at any point in time. Values close to 1 increase the proportion of high activity values.
Returns ndarray