Phase Tools

Define tools for extracting phase information from time series

Cosinor Analysis

The most popular technique for extracting phase information from time-series data is called cosinor analysis. The technique boils down to doing linear regression on cosine transformed data.

\[ y = A \cos(x + \beta) \]

or:

\[q(t,\phi) = a_1 \sin(\omega t) + a_2 \cos(\omega t) \]

In cosinor analysis the \(\omega\) term (the frequency) is taken as a known quantity and the \(a_{1,2}\) terms are fit to minimize the least square error.

Then the phase \(\phi\) is given by \(\arg(a_2 + i a_1)\)

We can find \(a_{1,2}\) directly from our data. First, lets define the terms we’re working with: \(y\) is the signal, and \(t\) represents the sampling times (same length as \(y\)). The matrix \(S\) is formed by taking the sin/cos of the time vectors and placing them in the columns \(S = [sin(\omega t); cos(\omega t)]\). Thus, we can write our system as:

\[ S a = y \]

where \(a = [a_1, a_2]\) are the two coefficients we want to solve for. This regression can be computed directly because the matrix \(S\) is orthogonal. This means that \(S^T S = I\), and we can solve the system with one matrix transpose multiplication.

\[\begin{align} Sa = y \\ S^T S a = S^T y, S^T S = I \\ a = S^T y \end{align}\]

Since \(S^T\) only has two columns we can write the matrix-vector product out for each component:

\[\begin{align} a_1 = \frac{ \sin(\omega t) \cdot y} { || \sin(\omega t) ||^2 } \\ a_2 = \frac { \cos(\omega t) \cdot y } { || \cos(\omega t) ||^2 } \end{align}\]

In circadian this functionality is implemented via the function cosinor and we use it as follows:

a_coeffs = cosinor(x_sample, y_sample_noisy, 100.0)
print(f"Recovered Cosinor Parameters {a_coeffs[0]:.4f} sin(omega t) + {a_coeffs[1]:.4f} cos(omega t)")
print(f"Phase Estimate: {cosinor_phase(a_coeffs):.4f} versus the true phase: {phi_true:.4f}")


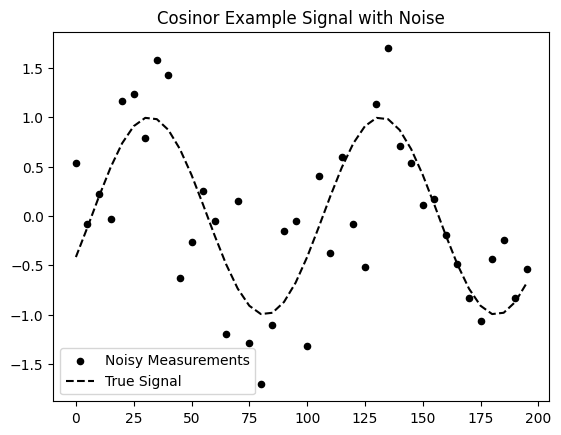
plt.scatter(x_sample,y_sample_noisy, color='k', s=20, label='Noisy Measurements')
plt.plot(x_sample, y_sample, ls = '--', color = 'k', label = 'True Signal')
plt.plot(x_sample, a_coeffs[0]*np.sin(2*np.pi/100.0 *x_sample) + a_coeffs[1]*np.cos(2*np.pi/100.0 *x_sample), ls = '--', color = 'r', label = 'Cosinor Fit');
plt.legend()
plt.title('Cosinor Example Signal with Noise');

Recovered Cosinor Parameters 0.8104 sin(omega t) + -0.2875 cos(omega t)
Phase Estimate: 1.9117 versus the true phase: 2.0000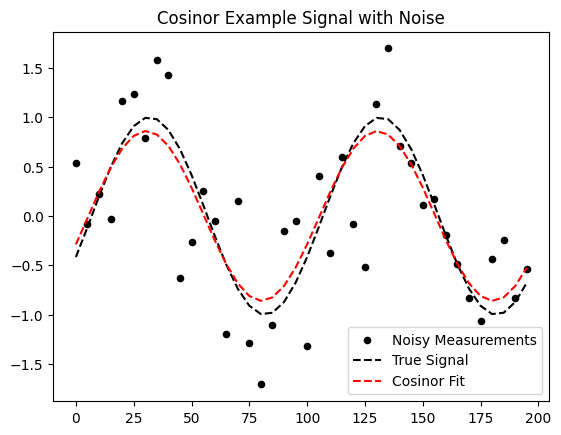

GOALS: Cosinor with gaps

One of the main challenges with the cosinor method is that it assumes that the data is continuous. This is not always the case. For example, if you are measuring a signal at a fixed time interval, but the signal is not present at all times, then you will have gaps in your data.

The GOALs algorithm is a modification of the cosinor method that allows for gaps in the data and is implemented as cosinor_goals on circadian.

phi_true = 2.0
x_sample = np.hstack((np.arange(0, 20, 1), np.arange(40, 60, 1)))
y_sample = f_signal_cosinor(x_sample, phi_true) 
y_sample_noisy = y_sample + np.random.normal(0, 0.5, x_sample.shape)

a_coeffs = cosinor_goals(x_sample, y_sample_noisy, 100.0)
print(f"Recovered GOALS Cosinor Parameters {a_coeffs[0]:.4f} sin(omega t) + {a_coeffs[1]:.4f} cos(omega t)")
print(f"GOALS Phase Estimate: {cosinor_phase(a_coeffs):.4f} versus the true phase: {phi_true:.4f}")


a_coeffs_plain = cosinor(x_sample, y_sample_noisy, 100.0)
print(f"Recovered Cosinor Parameters {a_coeffs_plain[0]:.4f} sin(omega t) + {a_coeffs_plain[1]:.4f} cos(omega t)")
print(f"Regular Cosinor Phase Estimate: {cosinor_phase(a_coeffs_plain):.4f} versus the true phase: {phi_true:.4f}")

x_fill = np.arange(0, 100, 1)
y_fill = f_signal_cosinor(x_fill, phi_true)
plt.scatter(x_sample,y_sample_noisy, color='k', s=20, label='Noisy Measurements')
plt.plot(x_fill, y_fill, ls = '--', color = 'k', label = 'True Signal')
plt.plot(x_fill, a_coeffs[0]*np.sin(2*np.pi/100.0 *x_fill) + a_coeffs[1]*np.cos(2*np.pi/100.0 *x_fill), ls = '--', color = 'r', label = 'GOALs Cosinor Fit');
plt.plot(x_fill, a_coeffs_plain[0]*np.sin(2*np.pi/100.0 *x_fill) + a_coeffs_plain[1]*np.cos(2*np.pi/100.0 *x_fill), ls = '--', color = 'b', label = 'Cosinor Fit');
plt.legend()
plt.title('Cosinor (GOALS) Example Signal with Noise');

Recovered GOALS Cosinor Parameters 0.4250 sin(omega t) + -0.3013 cos(omega t)
GOALS Phase Estimate: 2.1875 versus the true phase: 2.0000
Recovered Cosinor Parameters 0.6239 sin(omega t) + -0.1410 cos(omega t)
Regular Cosinor Phase Estimate: 1.7931 versus the true phase: 2.0000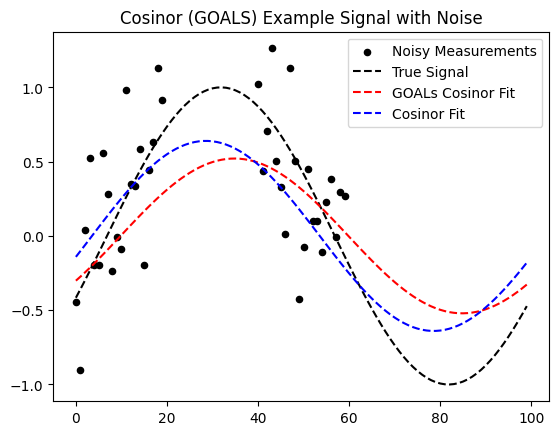

---

source

cosinor

 cosinor (t:<built-infunctionarray>, y:<built-infunctionarray>, tau:float)

Estimate the phase of a signal using cosinor analysis.

	Type	Details
t	array	time vector
y	array	signal vector
tau	float	period of cosinor analysis
Returns	float	phase estimate

---

source

cosinor_phase

 cosinor_phase (a:<built-infunctionarray>)

---

source

cosinor_goals

 cosinor_goals (t, y, tau:float)